摘要

本文证明了第一类和第二类高阶Stirling数的序列既是Pólya频率序列又是对数凹序列。然后，我们证明了与上述高阶Stirling数相关的多项式是q-log-凸或强q-log-凸的。进一步证明了与第一类2级斯特林数相关的线性变换保持对数凸性。

1 介绍

一个集合的集合划分是一个非空的不相交子集的集合，称为块，其并集为[n]。[n]的集合划分为k个非空块的个数由第二类斯特林数给出。如果，则令表示[n]中恰好有k个非空块的所有分区的集合。在整个过程中，我们将假设这些块按照最小元素的升序从左到右排列。给定一个分区，令表示的每个块中最小元素的集合。斯特林数的组合、算术和解析性质是众所周知的，例如参见[1,2]。斯特林数的经典推广来自组合设置，例如，通过对块的大小施加限制(参见[3])，以及从分析方法(参见[4])。

最近，Komatsu等人[5,6,7]开始了对更高水平(水平s)的Stirling数的组合研究。注意，这个序列是在1918年由Tweedie[8]首次出现的。给定一个正整数s，令表示有序s元组的个数，使得。这种数列称为第二类高阶斯特林数。或者，第二类更高阶的斯特林数可以定义为连接系数，表达式如下:

（1)

这个序列可以由递归关系确定

（2）

初始条件()和for。注意，对于，我们恢复了第二类的经典斯特林数。Domaratzki[9]将这种推广称为广义阶乘数，因为对于，序列通过等式与中心阶乘数T(n, k)相关，其中

给定一个正整数s，令表示多项式恒等式中的连接系数

（3）

这些数被称为第一类更高层次的Stirling数，最近有研究[7]。令表示[n]的排列集合。我们将假设排列以标准循环形式表示，即每个循环中首先是最小元素，循环按照最小元素的升序从左到右排列。如果，则表示恰好有k个循环的排列集合。给定中的一个排列，令表示的每个循环中最小元素的集合。给定一个正整数s，该序列计算有序s元组的个数，这样。

这个序列可以由递归关系确定

（4）

有初始条件，为。

第一类高阶Stirling数满足以下递推关系[6]:

（5）

此外，两种水平较高的Stirling数之间的正交关系(参见[5,6])为

和

克罗内克三角洲在哪里。

在这篇文章中，我们证明了与斯特林数相关的两种高阶序列是全正的、Pólya频率的、对数凹的或单峰的。我们还刻画了一些保持双对数凸性的线性变换。

2 主要结果

2.1 第二类高阶斯特林三角形的总正性

设为一个无穷矩阵。如果它所有阶次的子函数都是非负的，则称为r阶的全正函数(简称r阶)。如果它所有阶的次元都是非负的，我们称之为TP。例如，Pascal数组是一个TP矩阵[10,p.137]。全正矩阵在全正性理论中占有重要地位(参见[10,11,12])。

定理2.1

矩阵是TP。

证明

从两种高阶斯特林数之间的正交关系，得到了等式

如果和，则上述等式可以写成矩阵形式，其中

和

注意这是完全积极的。因此，通过对n的归纳法，我们利用经典的柯西-比奈公式推导出非负矩阵和是TP，该公式将任意的子矩阵的行列式表示为和的子矩阵的行列式的积和;详见Karlin[10]。这就完成了证明。

2.2 Pólya频率序列

设一个非负数的无穷数列。如果其为Toeplitz矩阵，则称为Pólya r阶频率序列(简称序列)

TP。若其Toeplitz矩阵为TP，则称为PF。如果无限序列是PF (PF, resp)，则称有限序列为PF (PF, resp)。

我们将使用Aissen, Schoenberg和Whitney[13]给出的以下结果，参见[10,p. 399]。

定理2.2

一个有限序列是PF当且仅当它的生成函数只有实零。

第一类高阶斯特林数的生成函数如(3)所示。因此，根据定理2.2，我们得到如下结果:

定理2.3

的每一行序列都是一个PF序列。

高阶n次的贝尔多项式定义为

注意，对于，我们恢复了经典的贝尔多项式([1])。现在我们引入多项式

注意，从(2)中，我们得到了递归式

（6）

引理2.4

对所有

（7）

的i阶导数是。

证明

众所周知，第二类斯特林数也定义为

（8）

Where, for和。由式(8)可知

的i阶导数是。

利用Harper方法[14，引理1]和引理2.4，我们可以得到如下类似的结果。

定理2.5

的每一行序列都是一个PF序列。

引理2.6

[15，引理2.2]设和为两个PF序列，且由乘积定义

然后，也是PF。

定理2.7

的每一列序列是一个PF序列。

证明

我们知道的列生成函数由

然后，根据引理2.6，列序列是PF，因为该序列也是PF。

设和分别为n次多项式f和g的实数零的非递增序列。多项式g与f相交，记为if[16]。

引理2.8

([16])设为满足下列条件的实多项式。

（1)
，其中是实多项式，使得或。
（2）
对于每个j, f和的所有0都是实数。
（3）
F和有相同符号的前导系数。

假设无论何时。那么F的所有0都是实数。

定理2.9

对于所有的高阶贝尔多项式都具有交错性质，即。

证明

从引理2.4和(6)中，我们取，，，，和。很明显，这些都是实多项式。而且，根据罗尔定理，和的所有零都是实数和。因此，引理2.8中的条件(2)对所有都成立。条件(3)很清楚。最后，高阶贝尔多项式的零都是实数和负数。因此，对于所有j，无论何时，这就完成了证明。

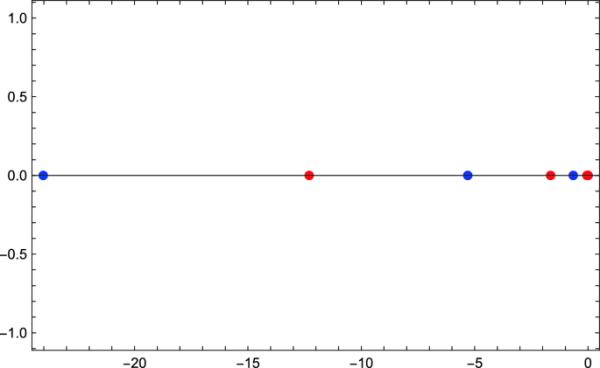
例2.10

在图1中，我们显示了多项式和的零点

图1

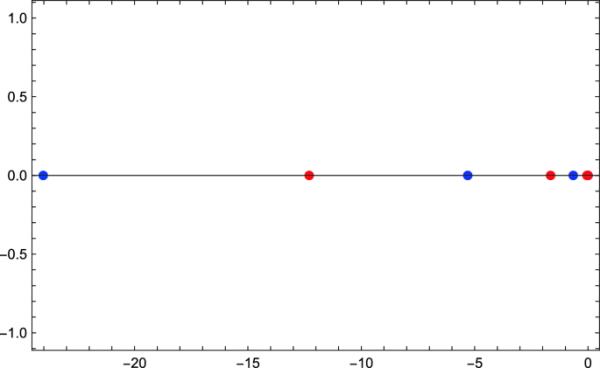
(红色)和(蓝色)的零点(联机色图)

2.3 Log-Co序列的空腔和单模性

如果对所有非负数序列都是对数凹的，它等价于(相关结果可参见[15,17,18])

(9)

显然，当且仅当序列为PF，即其Toeplitz矩阵为TP时，该序列是对数凹的(参见[19])。一个有限实数序列，如果存在一个指数，称为数列的模态，使数列增加到，并从此减小，则称其为单峰序列。很容易看出，如果一个序列是对数凹的，那么它是单峰的[15]。

从定理2.3和2.5，我们得到以下结果。

推论2.11

和的每一行序列都是对数凹的，因此是单峰的。

从定理2.1，我们也得到了下面的结果。

推论2.12

的每个列序列是对数凹的，因此是单峰的。

根据Su和Wang的方法[20，定理4]，我们可以建立如下结果:

定理2.13

设和b为正整数。序列是对数凹的，因此是单峰的。

证明

为了证明它是对数凹的，只需表明

这是

在哪里和。根据推论2.11和2.12，我们有

和

由此得出

（10）

另一方面，根据定理2.1

这意味着

（11）

因此，由(10)和式(11)可知

这是

这就完成了证明。

众所周知，第一类斯特林数的模态是最接近调和数的整数。J. Hammersley[21]证明了这一惊人的结果。因此，要找到第一类斯特林数具有更高阶的模态，我们需要以下引理。

引理2.14

([19])设多项式只有实根的正实数序列，即为PF序列。那么序列的每个模态都满足

其中和分别表示x的下限和上限。

定理2.15

序列的每个模态都满足

（12）

每个人。

证明

让。到(3)，我们有

利用引理2.14，我们有

另一方面，我们有

结果马上就出来了。

在上述定理的基础上，我们得到了J. Hammersley关于第一类斯特林数模态的结果。

例2.16

定理表明，对于和模态满足

实际上，是最大值，见图2。

图2

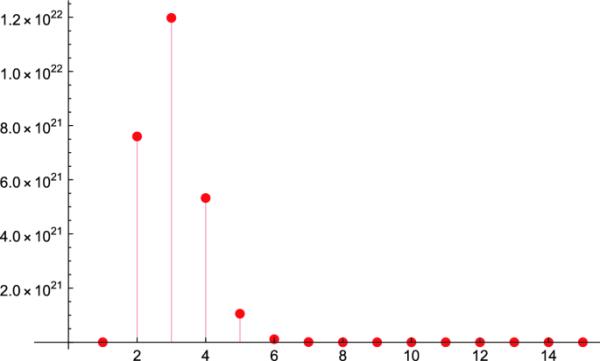
序列，为

2.4 强大的问-log-co行生成函数的维数

对于两个实数系数f(q)和g(q)的多项式，如果差值只有非负系数，则记为f(q)。对于多项式序列，它被称为q-log-凸(resp)。q-log-凹)

这一概念由Liu和Wang提出[22](Stanley首先提出)。多项式序列称为强q-log-凸序列。强q-log-凹)如果

参见Chen et al.[23]。显然，它们的多项式序列的强q-log-凸性暗示了q-log-凸性。然而，反之则不成立(参见[23])。很容易看出，如果序列是q-log-凸的，那么对于每个固定的非负数q，该序列是log-凸的。多项式的q-log-凹凸性和q-log-凸性已经得到了广泛的研究，例如参见[22,23,24,25]。

在接下来的两个定理中，我们讨论了两类高阶斯特林数的行生成函数的q-log凸性。

定理2.17

设为的行生成函数。那么多项式序列就是q-log-凸。

证明

由式(4)可知，的行生成函数满足以下递归式:

（13）

对于和，我们有

和

因此，和形成一个多项式的q-log-凸序列。现在假设它有非负系数。重复应用递归式(13)得到

因此，有非负系数。因此，通过归纳，是q-log-凸。

话2.18

对于，序列是对数凸的。

引理2.19

[26，引理2.6]给定三个非负序列，，且，如果和对递增，则

定理2.20

设为的行生成函数。那么多项式序列是强q-log-凸的。

证明

为了证明它是强q-log-凸的，它足以表明

对。由递归关系(7)和引理2.4，我们有

由此得出

（14）

注意到定理2.1是完全正的，我们推出

For和。因此，如果我们把and看作引理2.19中的and，那么我们得到

因此，通过(14)，

这就完成了证明。

2.5 保持对数凸性的线性变换

让我们考虑以下两个序列的线性变换:

（15）

和

（16）

其中是正实数的三角形数组。线性变换(15)保留了对数凸性(p。如果序列的对数凸性(相对于。的对数凹性意味着的对数凹性。我们还说，相应的三角形保持对数凸性(相对于。log-concavity)。线性变换(16)保留了双对数凸性。如果序列的对数凸性(相对于。的(log-凹凸性)和暗示的(log-凹凸性)。我们还说，相应的三角形保留了双对数凸性。双对数凹度)。现在定义by的倒数三角形

如果两个三角形都保持对数凸性，则三角形保持双对数凸性。Menon[27]证明了在普通卷积下对数凹性是保持的。然而，两个对数凸序列的普通卷积不一定是对数凸的。即使对数凸序列的部分和序列一般也不是对数凸的。另一方面，Davenport和Pólya[28]表明，在二项卷积下，对数凸性保持不变。这种卷积也保留了对数凹性，参见Walkup[29]。也证明了q-二项卷积保留了对数凹性，参见[30]。在[31,32,33,34]中，作者分别建立了二项式系数和p、q二项式系数的保对数凸性和保对数凹性。

Liu和Wang[22]在三角形阵列上得到了保证线性变换(15)保持对数凸性的充分条件。给定一个三角形数组，定义为

（17）

式中，，和。Liu和Wang的充分条件表述如下: